Subiecte Evaluare Nationala 2024 Matematica, rezolvari

Subiecte (Gorj) – varianta 7:

REZOLVAREA SUBIECTELOR DE EXAMEN EVALUARE NATIONALA 2024 MATEMATICA

SUB I.

1. 8 + 14:2 = 8 + 7 = 15 => raspuns corect b)
2. Reducere de 20% inseamna sa inmultim 200 lei cu 80% => 200 x 80/100 = 2 x 80 = 160 lei
   • Metoda 2: 200 x 20/100 = 2 x 20 = 40 lei => scadem din 200 cei 40 lei => 160 lei => raspuns corect c)
3. I intersectat cu J va fi intervalul (4,6] deoarece 4 < 6 => raspuns corect d)
4. 5,(024) = 5,024024024 … , 5,(24) = 5,242424 … , 5,2(4) = 5,244444 … iar 5.24 nu are perioada. Cel mai mare numar este, dupa comparatia zecimalelor, 5,2(4) => raspuns corect c)
5. Daca o suma de 2 module de numere reale este 0, atunci fiecare modul va fi 0. Deci a+3 = 0 => a =-3 si b-4 = 0 => b = 4. Suma numerelor a si b va fi: a+b = -3 + 4 = 4 – 3 = 1 => raspuns corect c)
6. Numarul x = 1 este solutie a ecuatiei date daca verifica ecuatia: 2x + 3 = 4x + 1 adica 2 + 3 = 4 + 1 adevarat => raspuns corect a)

SUB II.

1. BC = 4, AD = 4BC = 16 => AB = CD = (16-4)/2 = 8-2 = 6 => raspuns corect b)
2. ABC triunghi isoscel si C = 40^o => B = 40^o => unghiul BAC = 180^o – 2 x 40^o = 100^o => unghiul exterior va fi de 180^o – 100^o = 80^o
   • Metoda 2: Deoarece B + C = 2 x 40^o = 80^o => raspuns corect c)
3. In triunghiul ABC: A = 43^o, C = 51^o => B = 180^o – (43^o+51^o ) = 86^o Se observa MNBP paralelogram, deci unghiul NMP = unghiul B = 86^o => raspuns corect c)
4. In paralelogramul ABCD daca M este mijlocul lui AB rezulta ca aria (ABC) = 2 x aria (ACM) = 20 cm² Dar aria(ABCD) = 2 x aria (ABC) = 40 cm² => raspuns corect d)
5. Deoarece AC este diametru si C se afla pe cerc => triunghiul ABC dreptunghic in C. Cum unghiul BAC = 30^o => coarda BC = ipotenuza / 2 = AC / 2 = raza = 6 cm => raspuns corect a)
6. In orice cub ABCDA’B’C’D’ avem AC si AD’ diagonale in patrate congruente, egale si cu CD’ => triunghiul ACD’ echilateral => unghiul cerut este de 60^o => raspuns corect b)

SUB III.

1. • a) Daca ar fi 30 de elevi, conform ipotezei: 30 – cei 3 elevi in picioare = 27 nu se pot aseza cate 2 in banca deoarece 27 este numar impar
   • b) Notam cu e = numarul de elevi si b = numarul de banci. Avem relatiile: 2b + 3 = e = 4(b-6) + 1 (scadem numarul de banci cu 5 si adaugam elevul care sta singur intr-o banca). Rezolvam ecuatia 2b+3 = 4b-24+1 => 2b + 26 = 4b => 2b = 26 => b = 13 (banci) si e = 26 + 3 = 29 (elevi). Ca si verificare: daca se aseaza cate 2 in cele 13 banci, raman 3 elevi in picioare (CORECT) iar daca se aseaza cate 4 elevi in banci, raman 5 banci libere si o banca cu un elev (CORECT) deoarece 4 x 7 banci + 1 elev intr-o banca = 29
2. • a) Cea mai simpla metoda este sa calculam intai produsul: (x-1)(x-2) = x² – 2x – x + 2 = x² – 3x + 2
   • Metoda 2: Putem descompune astfel: x² – 3x + 2 = x² – x – 2x + 2 = x(x-1) – 2(x-1) = (x-1)(x-2)
   • b) Ca sa luam punctaj partial, calculam E(n) = [ 1/ (x-1)(x-2) + 1/(x-1) ] (x² – 4) = (x² – 4) (1 + x – 2)/(x-1)(x-2) = (x-2)(x+2) (x-1)/(x-1)(x-2) = x + 2 Atunci: N = 5/E(n) = 5 / (n+2) este numar natural doar daca n+2 divide 5, adica n+2 = {1,5} => scadem 2: n = {-1, 3} ambele variante numere intregi.
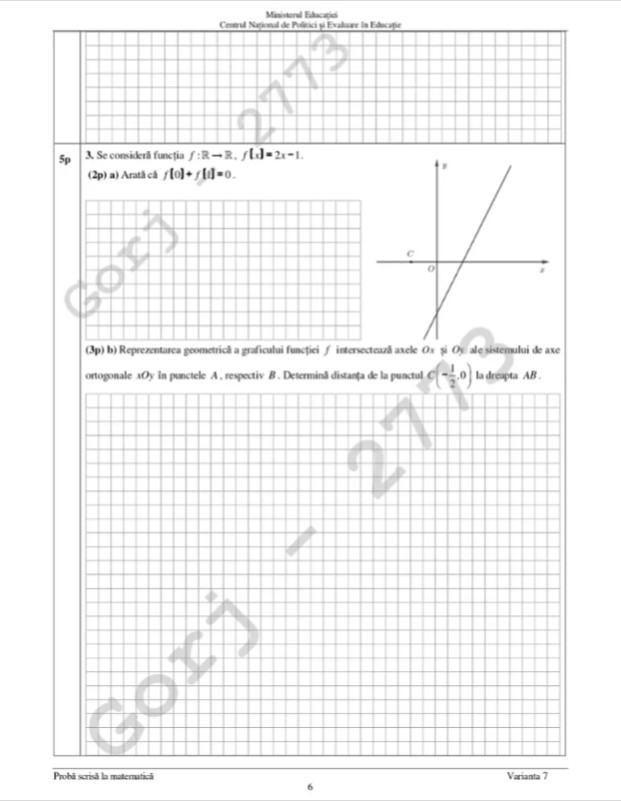
3. • a) f(0) + f(1) = 2×0 – 1 + 2×1 – 1 = -1 + 2 -1 = 0
   • b) Ca sa luam punctaj partial, determinam intersectiile graficului cu axele
   • Gf inters Ox: rezolvam f(x) = 0 => 2x – 1 = 0 => 2x = 1 => x = 1/2 deci A(1/2, 0)
   • Gf inters Oy: calculam f(0) = -1 => B(0,-1)
   • Se observa, deoarece C(-1/2, 0), ca triunghiul ABC este isoscel (cea mai simpla metoda de demonstrare: OA = OC si BO va si si inaltime si mediana) = (alta metoda: triunghiurile AOB si BOC sunt congruente, caz de congruenta cateta-cateta)
   • Aflam aria triunghiului ABC in 2 moduri diferite. Odata este egala cu (inaltimea BO x baza AC) / 2 = 1 x (1/2 + 1/2) / 2 = 1 x 1 / 2 = 1/2 (alta metoda: aria (ABC) = 2 aria (AOB) = 2 x (1/2 x 1) / 2 = 1 /2 )
   • Deoarece ne intereseaza distanta de la C la AB, vom avea: aria (ABC) = dist x AB / 2
   • Aflam AB conform teoremei Pitagora in triunghiul AOB => AB² = AO² + OB² = 1/4 + 1 = 5/4 => AB = √5 / 2 (deoarece √4 = 2)
   • Aria(ABC) = 1/2 = dist x √5 / 2 / 2 => raspuns final: dist = 2 / √5 = 2√5 / 5
4. • a) Deoarece triunghiurile DAC si EBC sunt dreptunghice si unghiul C este unghi comun => unghiul EBC = 90^o – C si unghiul DAC = 90^o – C => unghiul EBC = unghiul DAC
   • b) Triunghiurile AHE si BHD sunt asemenea deoarece sunt dreptunghice si au unghiul opus la varf BHD = AHE, dar si triunghiurile BHD si ADC (sau ACD) sunt asemenea => conform asemanarii: BD/ AD = BH /AC = HD / CD. Stim ca CD = BD si AD = BC din ipoteza. Deci 1/2 = DH / CD => DC = 2 DH deci AD = 4 DH. De aici prin scadere: AH = AD- DH = 4 DH – DH = 3 DH deci AH = 3 DH
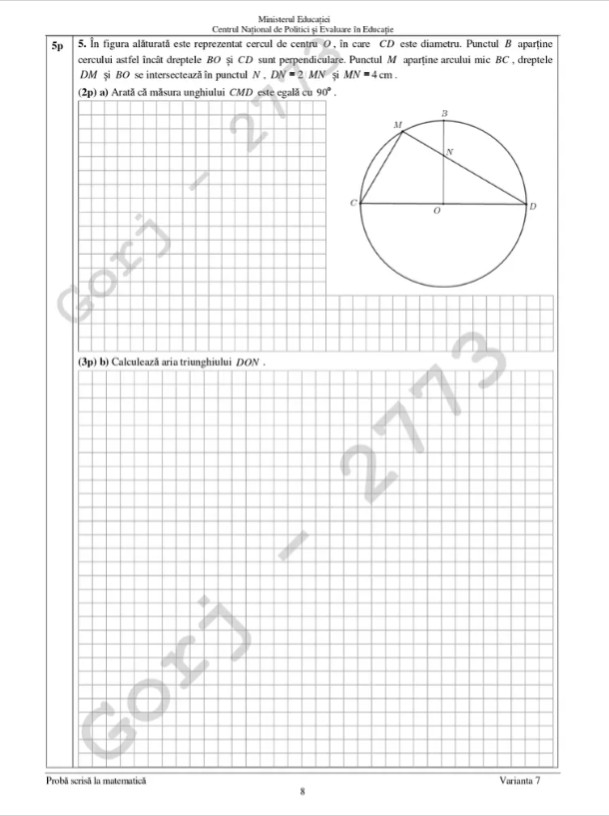
5. • a) Deoarece CD este diametru si M apartine cercului => triunghiul CDM dreptunghic in M => unghiul CMD = 90^o
   • b) Deoarece triunghiurile DMC si DON sunt dreptunghice si au unghiul comun D => asemanarea triunghiurilor DMC si DON. Din asemanare: DN / CD = NO / MC = OD / MD.
   • Dar MD = 4 + 8 = 12, ND = 8 si CD = diametru = 2R rezulta: 8 / 2R = NO / MC = R / 12
   • Deci 2R² = 8 x 12 = 96, adica R² = 48, deci R = 4√3
   • Aria (DON) = DO x ON / 2
   • DO = 4√3 si ND = 8 => conform teoremei lui Pitagora: NO² = 64 – 48 = 16, deci NO = 4
   • Aria (DON) = 4√3 x 4 / 2 = 8 √3 cm²
6. • a) Aria laterala poate fi calculata ca fiind 3 x aria (A’ABB’) unde A’ABB’ = dreptunghi.
   • Aria (A’ABB’) = 12 x 3√3 = 36√3 deci aria laterala prisma = 3 x 36√3 = 108 √3 cm²
   • b)
   • VARIANTA SIMPLA:
   • Aratam ca triunghiul A’B’C este isoscel (vezi mai jos) si fie N mijlocul lui A’B’. Triunghiul CMN este dreptunghic in M deoarece MN || BB’ si CM perpendicular pe planul (A’MB’) = (A’ABB’)
   • In acest caz distanta ceruta este data de inaltimea in triunghiul dreptunghic CMN.
   • Avem CM = 6√3, MN = 3√3 si CN = √135 (teorema Pitagora) => distanta = CM x MN / CN = 6x3x√3x√3/ √135 = 18×9 / √135 = 6√15/5
   • VARIANTA COMPLICATA:
   • Consideram piramida cu varful in M si baza A’B’C egala cu piramida cu varful in C si baza A’B’M.
   • Aria (A’B’M) = BB’ x A’B’ / 2 = 3√3 x 12 / 2 = 18 √3 cm²
   • Volum piramida (M A’B’C) = 1/3 x CM x aria (A’B’M) = 1/3 x 12√3 / 2 x 18√3 = 12 x 18 x 3 / 6 = 108 cm³
   • Volum piramida (M A’B’C) = 1/3 x dist x aria (A’B’C)
   • Dar CA’ = CB’ => triunghiul A’B’C este isoscel, B’C ² = 144 + 27 = 171. Aflam inaltimea CN in triunghiul A’B’C => CN² = B’C ² – B’N² = 171 – 36 = 135 => aria (A’B’C) =√135 x 12 / 2 = 6√135 cm²
   • Atunci: 1/3 x 6√135 x dist = 108 deci dist = 108 / 2√135 = 54 / √135 = 54 / 3√15 = 18/√15 = 18√15 / 15 = 6√15/5