REZOLVARE SUBIECT Evaluare Nationala, Matematica, 2025

Subiecte date la Evaluarea Nationala din 2025, 25.06.2025:

REZOLVARE SUBIECT I.

1. 4+12:2 = 4 + 6 = 10 => raspuns c)
2. 3a = 2×2 => 3a = 4 => a = 4/3 => a/4 = 1/3 => raspuns a)
3. -2 x 5 = -10 => raspuns a)
4. 6x-2=1 => 6x = 3 => x = 3/6 = 1/2 =>raspuns d)
5. a² = 3² + 4² => a = 5, b² =3² x 4² =>b= 3×4 = 12 deci suma a+b = 5+12 = 17 =>raspuns a)
6. Doar 4 elevi au obtinut 80 pct => fals => raspuns b)

REZOLVARE SUBIECT II.

1. AD = 12 = 3x AB => AB = 4 => AC = 8 => raspuns d)
2. <AOC = 120^o => <AOB = 40^o => <AOM = 80^o => raspuns d)
3. Triunghiul ABC este isoscel cu <A = 120^o => <B = <C = (180^o – 120^o )/2 = 30^o . Triunghiul AEC este isoscel cu AE = EC = 4 iar in triunghiul dreptunghic AEB aplicam teorema 90-30 => BE = 2 CE = 8 => BC = 4 + 8 = 12 raspuns b)
4. AB = 3BC => L = 3 l iar perimetru dreptunghi P = 2L + 2l = 6l + 2l = 8l = 32 => l = 4 iar L = 12. Aria = L x l = 12 x 4 = 48 cm² raspuns c)
5. <BDC = arc mare BC / 2 deoarece este unghi cu varful pe cerc. Arcul mic BC = 60^o x 2 = 120^o => arc mare BC = 360^o – 120^o = 240^o => <BDC = 120^o raspuns c)
6. AB = 6 => raza R = 6/2 = 3 cm. Generatoarea G = AB = 6 cm. Arie laterala con = pi x R x G = 3x 6 pi = 18 pi cm² rapuns a) OBS: Nu este nevoie de inaltimea conului = inaltime triunghi echilateral!

REZOLVARE SUBIECT III.

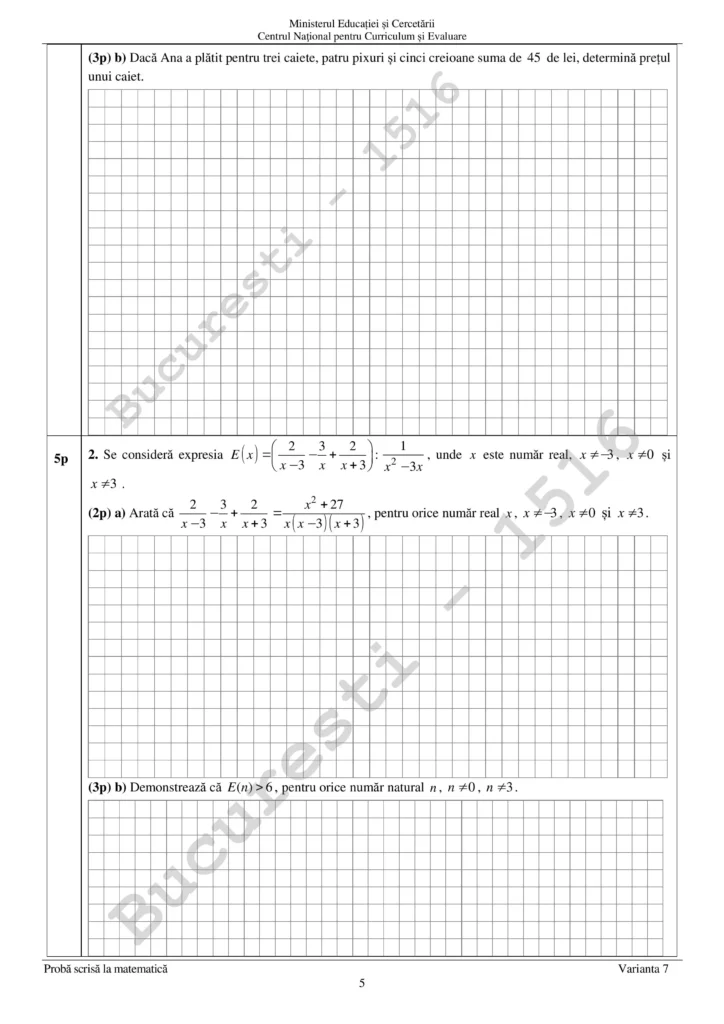
1. a) Notam cu p = pretul unui pix si x = pretul unui caiet si y = pretul unui creion. Presupunem ca 8p = 5c.

Stim ca p = 75% x = 3x/4 iar y = 40% p = 4p/10.

Inmultim pretul pixului cu 8 => 8p = 24x/4 = 6x diferit de 5x => afirmatia este falsa

1. b) Cu notatiile precedente:

3x + 4p + 5y = 45

p = 3x/4

y = 4p/10 = 3x/10 => inlocuim in prima relatie: 3x + 12x/4 + 15x/10 = 45

3x + 3x + 1.5 x = 45 => 7.5 x = 45 => x = 6 lei

2. a) Se aduce la acelasi numitor: x (x-3) (x+3) => 2x(x+3) – 3 (x-3)(x+3) +2x(x-3) = 2x²+6x – 3(x²-9) +2x² – 6x = 2x² +6x – 3x² +27 + 2x² – 6x = x² +27

2. b)Conform a) expresia va fi E(x) = (x² +27)(x² – 3x)/x(x-3)(x+3) = (x² +27)/(x+3)

E(n)>6 <=> x² +27 > 6x+18 <=> x² – 6x + 9 > 0 <=> (x-3)² > 0, adevarat pentru n natural nenul diferit de 3, deoarece pentru n = 3 obtinem 0 > 0 fals

3. a) f(x) = 2x-4 => f(2) – f(0) = 2×2 – 4 – (2×0 – 4) = 4 – 4 + 4 = 4

b) {A} = intersectia Gf cu axa Ox => rezolvam ecuatia f(x) = 0 ca sa aflam abscisa punctului A => 2x=4 => x = 2 => A(2,0)

{B} = intersectia Gf cu axa Oy => calculam f(0)=0-4 = -4 ca sa aflam ordonata punctului B => B(0,-4).

{C} = sim _Oy A => C(-2,0)

AB² = (0-2)² + (-4-0)² = 4 + 16 = 20

AC² = (-2-2)² + 0² = 16

BC² = (-2-0)² + (0+4)² = 4 + 16 = 20

Perimetru ABC = AB + AC + BC = 4 + 2√5 + 2√5 = 4√5 + 4 = 4(√5 + 1)

4. a) AC = diagonala in patrat = AB√2

Perimetru ABCD = 48 => AB = 48/4 = 12 => AC = 12√2 => Perimetru ACE = 3 x 12√2 = 36√2

4. b)Triunghiul ADC este dreptunghic isoscel => <DAE = < DCE = 15^o

Triunghiurile ADE si DCE sunt congruente deoarece: <DAE = < DCE = 15^o , AE = EC si AD = DC (caz LUL)

Aria ADE = (Aria ACE – Aria ADC)/2

Aria ACE = AC²√3/4 = 144 x 2 x √3/4 = 288√3/4 = 72√3

Aria ADC = Aria ABCD / 2 = 144 / 2 = 72

Deci Aria ADE = (72√3 – 72) / 2 = 36√3 – 36

Dar Aria ADE = DT x AE/2 unde DT = d(D, AE) => DT x AE = 72√3 – 72 => DT = (72√3 – 72)/ AE

Deci DT = (72√3 – 72) / 12√2 = (6√3 – 6)/√2 = (6√6 – 6√2)/2 = 3√6 – 3√2 = 3√2(√3 – 1)

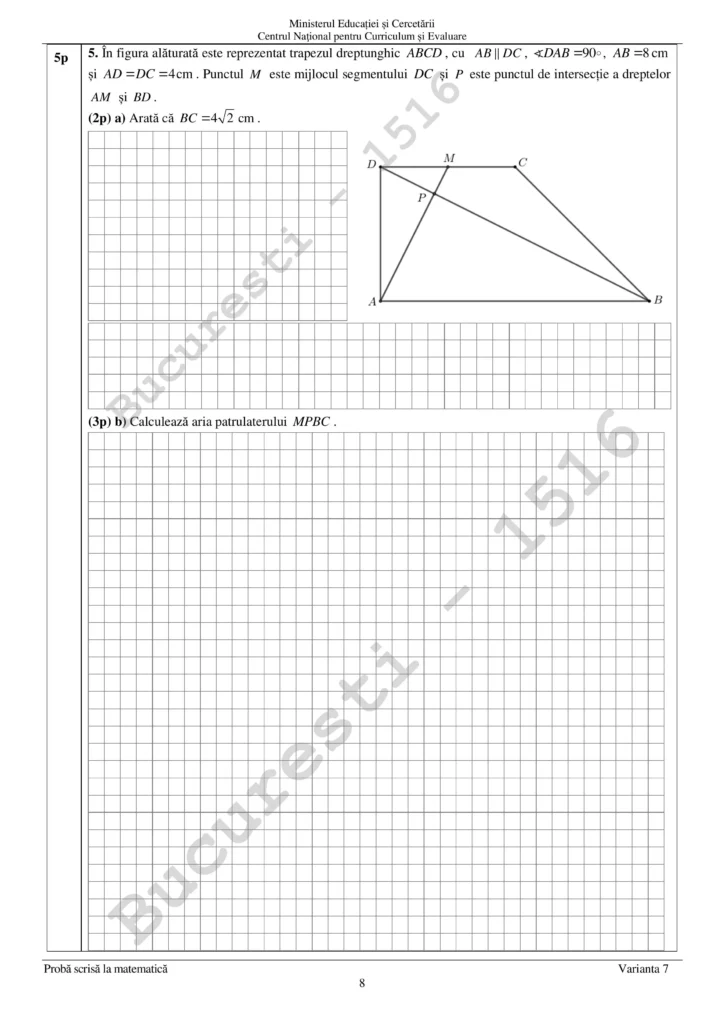
5. a) Triunghiul DAB este dreptunghic, AB=8 iar AD=DC=4

M mijloc CD => DM=MC= 2

Ducem CN inaltime in trapez => CN = AD = 4 si BN = AB – AN = 8 – 4 = 3

Triunghiul BCN va fi dreptunghic isoscel => ipotenuza BC = CN√2 = 4√2

5. b) Arie MPBC = Arie ABCD – (Arie ADM + Arie APB)

Arie ABCD = (AB+CD) x CN / 2 = (8+4)x4/2 = 48/2 = 24

MD || AB si <CDB = <DBA (alt int) => triunghiurile DPM si APB sunt asemenea cu raport de asemanare = DM/AB = 2/8 = 1/4

Atunci si raportul inaltimilor va fi tot de 1/4

Notam cu h inaltimea din P in triunghiul DPM si cu H = inaltimea din P in triunghiul APB

h + H = CN = 4 si H = 4h => 5h = 4 => h = 4/5 => H = 16/5 => Arie APB = H x AB / 2 = 16/5 x 8 /2 = 64/5

Arie ADM = AD x DM/ 2 = 4×2 / 2 = 4

Deci Arie MPBC = 24 – (4+64/5) = 24 – 84/5 = 36/5 = 7.2

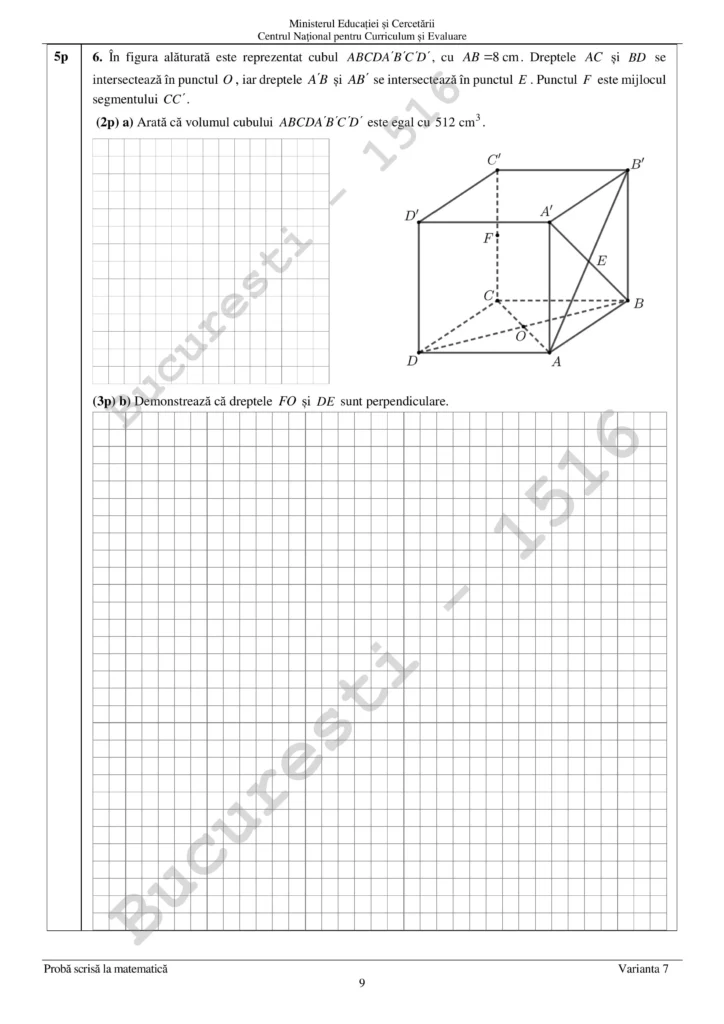
6. a) Volum cub = l ³ = 8 ³ = 8x8x8 = 64×8 = 512 cm³

6. b) Notam cu O’ centrul cubului. Deoarece CC’ || OO’ si CC’ = OO’ => CC’O’O este patrat =>FO || C’O’ = C’A (ca si drepte)

Aratam ca C’A perpendicular pe DE. Dar C’D || AE => figura C’DAE este trapez dreptunghic deoarece DA perpendicular pe planul (ABB’)

AE = C’D /2

Trapezul dreptunghic C’DAE este ortodiagonal <=> inaltimea = medie geometrica a bazelor

Cum inaltimea in trapez = AD = 8 si Mg(AE, DC’) = √(4√2)x(8√2) = √64 = 8 => AC’ perpendicular pe DE